Learning to Understand: Identifying Interactions via the Mobius Transform

Poster

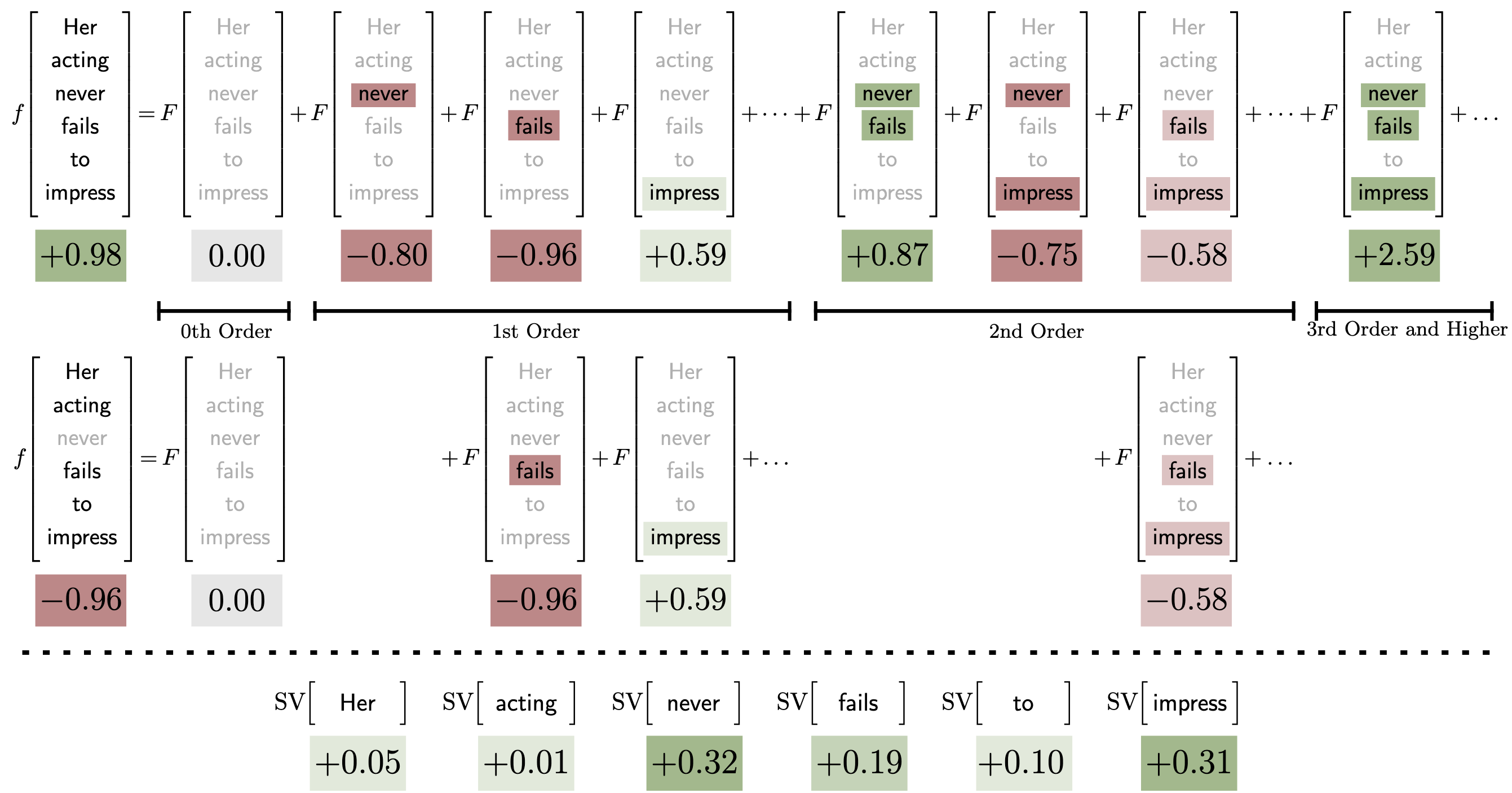
Abstract: One of the key challenges in machine learning is to find interpretable representations of learned functions. The Mobius transform is essential for this purpose, as its coefficients correspond to unique importance scores for sets of input variables. This transform is closely related to widely used game-theoretic notions of importance like the Shapley and Bhanzaf value, but it also captures crucial higher-order interactions. Although computing the Mobius Transform of a function with $n$ inputs involves $2^n$ coefficients, it becomes tractable when the function is sparse and of low degree as we show is the case for many real-world functions. Under these conditions, the complexity of the transform computation is significantly reduced. When there are $K$ non-zero coefficients, our algorithm recovers the Mobius transform in $O(Kn)$ samples and $O(Kn^2)$ time asymptotically under certain assumptions, the first non-adaptive algorithm to do so. We also uncover a surprising connection between group testing and the Mobius transform. For functions where all interactions involve at most $t$ inputs, we use group testing results to compute the Mobius transform with $O(Kt\log n)$ sample complexity and $O(K\mathrm{poly}(n))$ time. A robust version of this algorithm withstands noise and maintains this complexity. This marks the first $n$ sub-linear query complexity, noise-tolerant algorithm for the Mobius transform. In several examples, we observe that representations generated via sparse Mobius transform are up to twice as faithful to the original function, as compared to Shapley and Banzhaf values, while using the same number of terms.